C++ C++ C++七大经典排序算法详解 serverDream&SepiaTruck34735 2024-01-30 2024-02-02 C++七大经典排序算法详解 前言:排序是将一组数据,按照指定的顺序或要求来进行排列的过程。是数据结构相关课程和内容较为重要和核心的内容之一,常常作为考试题和面试题目来考察学生和面试者,因此熟练掌握经典的排序算法 原理和代码实现是非常重要的
各种排序算法动图解析请参考
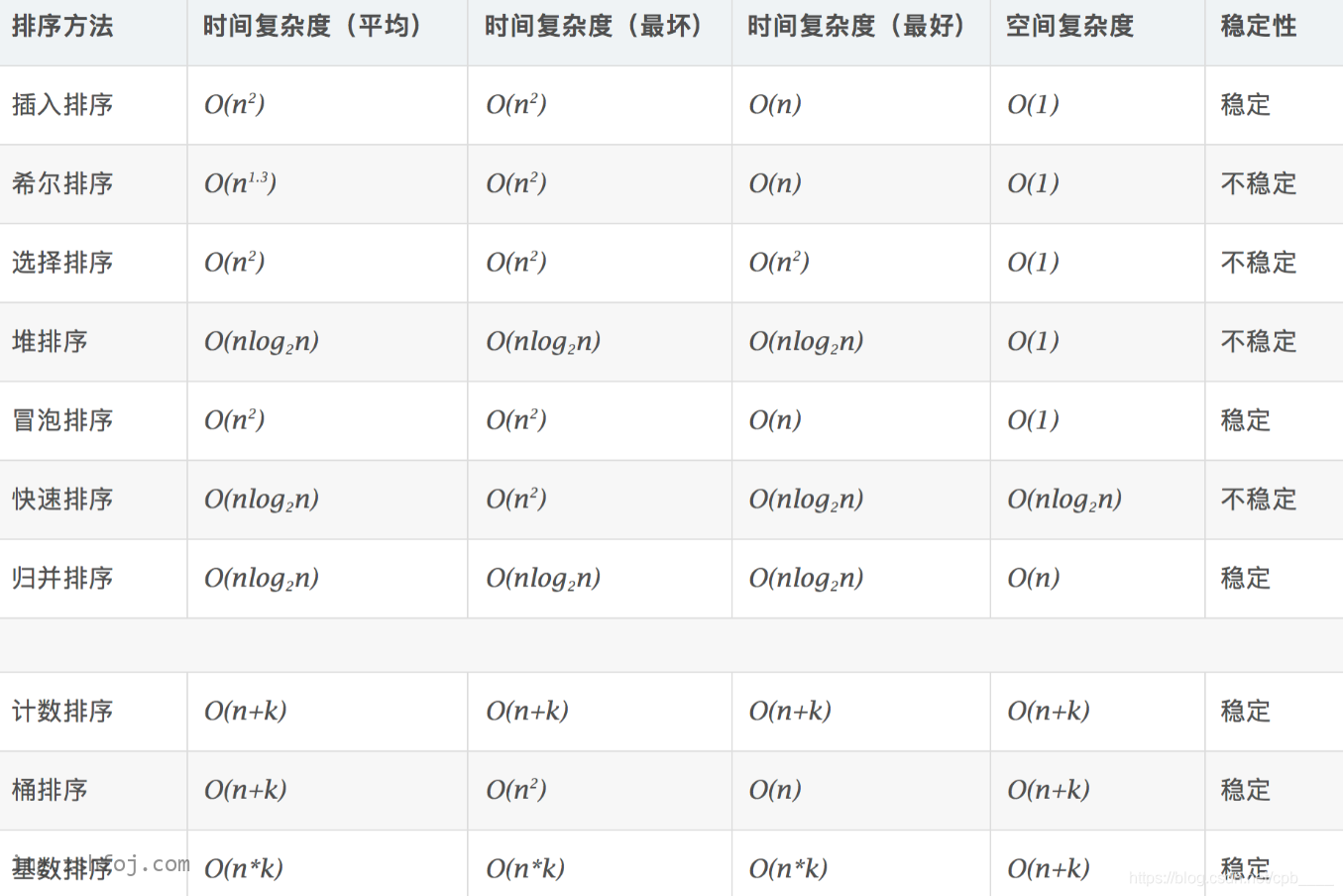
各种排序算法复杂度对比 冒泡排序 :两两比较,将大的元素不断后移;
冒泡排序法 冒泡排序是所有排序算法中相对简单且容易理解的算法,它的核心思想:通过for循环不断遍历需要排序的元素,依次比较相邻的两个元素,若不满足指定的顺序(可以从大到小排序,也可以反过来),就交换两个元素,直至完成排序。
1.比较相邻的元素。如果第一个比第二个大,就交换它们两个;
2.对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
3.针对所有的元素重复以上的步骤,除了最后一个;
4.重复步骤1~3,直到排序完成。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 void BubbleSort (int arr[], int n) for (int i = 0 ; i < n - 1 ; i++) { for (int j = 0 ; j < n - i - 1 ; j++) { if (arr[j] > arr[j + 1 ]) { int temp = arr[j]; arr[j] = arr[j + 1 ]; arr[j + 1 ] = temp; } } } }
冒泡排序优化: 用一个bool类型的变量来作为标志位,标记在某一轮遍历中是否发生过元素交换,如果未发生元素交换则证明当前数组已经排序完毕,直接中断此次循环。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 void BubbleSort (int arr[], int n) for (int i = 0 ; i < n - 1 ; i++) { bool flag = true ; for (int j = 0 ; j < n - i - 1 ; j++) { if (arr[j] > arr[j + 1 ]) { int temp = arr[j]; arr[j] = arr[j + 1 ]; arr[j + 1 ] = temp; flag = false ; } } if (flag) break ; } }
选择排序 选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
1.初始状态:无序区为R[1…n],有序区为空;
2.第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1…i-1]和R(i…n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1…i]和R[i+1…n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
3.n-1趟结束,数组有序化了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 void SelectionSort (int arr[],int len) for (int i = 0 ; i < len; i++) { int min = i; for (j = i + 1 ; j < len; j++) { if (a[j] < a[min]) min = j; } int temp = a[min]; a[min] = a[i]; a[i] = temp; } }
插入排序 插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
1.从第一个元素开始,该元素可以认为已经被排序;
2.取出下一个元素,在已经排序的元素序列中从后向前扫描;
3.如果该元素(已排序)大于新元素,将该元素移到下一位置;
5.将新元素插入到该位置后;
6.重复步骤2~5。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 void insertSort (int a[], int n) for (int i = 1 ; i < n; i++) { if (a[i] < a[i-1 ]) { int j = i-1 ; int x = a[i]; while (j >= 0 && x < a[j]) { a[j+1 ] = a[j]; j--; } a[j+1 ] = x; } } }
希尔排序 简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
1.选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
2.按增量序列个数k,对序列进行k 趟排序;
3.每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 void shellSort (int a[], int n) int i,j,gap; for (gap = n / 2 ; gap > 0 ; gap /= 2 ) { for (i = 0 ;i < gap; i++) { for (j = i + gap; j < n; j += gap) { if (a[j] < a[j - gap]) { int tmp = a[j]; int k = j - gap; while (k >= 0 && a[k] > tmp) { a[k + gap] = a[k]; k -= gap; } a[k + gap] = tmp; } } } } }
1 2 3 4 5 6 7 8 9 10 11 12 13 void shellsort (int arr[], int n) for (int gap = n; gap >= 1 ; gap /= 2 ) { for (int i = gap; i < n; i += gap) { int temp = arr[i]; int pre = i - gap; while (pre >= 0 && arr[pre] > temp) { arr[i] = arr[pre]; pre -= gap; } arr[pre + gap] = temp; } } }
归并排序 归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
1.把长度为n的输入序列分成两个长度为n/2的子序列;
2.对这两个子序列分别采用归并排序;
3.将两个排序好的子序列合并成一个最终的排序序列。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 void Merge (int arr[], int n) int temp[n]; int b = 0 ; int mid = n / 2 ; int first = 0 , second = mid; while (first < mid && second < n) { if (arr[first] <= arr[second]) temp[b++] = arr[first++]; else temp[b++] = arr[second++]; } while (first < mid) temp[b++] = arr[first++]; while (second < n) temp[b++] = arr[second++]; for (int i = 0 ; i < n; ++i) arr[i] = temp[i]; } void MergeSort (int arr[], int n) if (n <= 1 ) return ; if (n > 1 ) { MergeSort (arr, n / 2 ); MergeSort (arr + n / 2 , n - n / 2 ); Merge (arr, n); } }
快速排序(Quick Sort) 快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
1.从数列中挑出一个元素,称为 “基准”(pivot);
2.重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
3.递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 void Quicksort (int arr[], int low, int high) if (low < high) { int i = low; int j = high; int key = arr[i]; while (i < j) { while (i < j && arr[j] >= key) j--; if (i < j) arr[i] = arr[j]; while (i < j && arr[i] <= key) i++; if (i < j) arr[j] = arr[i]; } arr[i] = key; Quicksort (arr, low, i - 1 ); Quicksort (arr, i + 1 , high); } }
堆排序(Heap Sort) 堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
1.将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
2.将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
3.由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 #include "stdafx.h" #include <iostream> using namespace std;void swap (int arr[], int a, int b) int temp = arr[a]; arr[a] = arr[b]; arr[b] = temp; } void adjustHeap (int arr[], int i, int length) int temp = arr[i]; for (int k = i * 2 + 1 ; k<length; k = k * 2 + 1 ) { if (k + 1 <length&&arr[k]<arr[k + 1 ]) { k++; } if (arr[k] >temp) { arr[i] = arr[k]; i = k; } else { break ; } } arr[i] = temp; } void Heapsort (int arr[], int length) for (int i = length / 2 - 1 ; i >= 0 ; i--) { adjustHeap (arr, i, length); } for (int j = length - 1 ; j>0 ; j--) { swap (arr, 0 , j); adjustHeap (arr, 0 , j); } } int main () int arr[9 ] = { 9 ,8 ,7 ,6 ,10 ,4 ,3 ,2 ,1 }; Heapsort (arr, 9 ); for (int i = 0 ; i<9 ; i++) cout << arr[i] << " " ; cout << endl; return 0 ; }
关于 本篇文章作者是SepiaTruck34735 。
serverDream&SepiaTruck34735
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 serpblog !