C++数据结构1节-队列讲解+练习

serverDream&SepiaTruck347352024-02-062024-02-06

队列（queue）

本页面介绍和队列有关的数据结构及其应用。

引入

队列本着“先进后出”（FIFO）的原则，是一种具有「先进入队列的元素一定先出队列」性质的表。由于该性质，队列通常也被称为先进先出（first in first out）表，简称 FIFO 表。
下面是队列的示意图：

数组模拟队列

通常用一个数组模拟一个队列，用两个变量标记队列的首尾。

1	int q[SIZE], ql = 1, qr;

插入元素：q[++qr] = x;
删除元素：ql++;
访问队首：q[ql]
访问队尾：q[qr]
清空队列：ql = 1; qr = 0;

双栈模拟队列

还有一种方法是使用两个栈来模拟一个队列。

这种方法使用两个栈 F, S 模拟一个队列，其中 F 是队尾的栈，S 代表队首的栈，支持 push（在队尾插入），pop（在队首弹出）操作：

push：插入到栈 F 中。
pop：如果 S 非空，让 S 弹栈；否则把 F 的元素倒过来压到 S 中（其实就是一个一个弹出插入，做完后是首尾颠倒的），然后再让 S 弹栈。
容易证明，每个元素只会进入/转移/弹出一次，均摊复杂度 O(1)。

C++ STL 中的队列

C++ 在 STL 中提供了一个容器 std::queue，使用前需要先引入头文件。

STL 中的 queue 容器提供了一众成员函数以供调用。其中较为常用的有：

元素访问

q.front() 返回队首元素
q.back() 返回队尾元素
修改
q.push() 在队尾插入元素
q.pop() 弹出队首元素
容量
q.empty() 队列是否为空
q.size() 返回队列中元素的数量
此外，queue 还提供了一些运算符。较为常用的是使用赋值运算符 = 为 queue 赋值。

循环队列

使用数组模拟队列会导致一个问题：随着时间的推移，整个队列会向数组的尾部移动，一旦到达数组的最末端，即使数组的前端还有空闲位置，再进行入队操作也会导致溢出（这种数组里实际有空闲位置而发生了上溢的现象被称为「假溢出」）。

解决假溢出的办法是采用循环的方式来组织存放队列元素的数组，即将数组下标为 0 的位置看做是最后一个位置的后继。（数组下标为 x 的元素，它的后继为 (x + 1) % SIZE）。这样就形成了循环队列。

例题

#

题目背景

NOIP2010 提高组 T1

题目描述

小晨的电脑上安装了一个机器翻译软件，他经常用这个软件来翻译英语文章。

这个翻译软件的原理很简单，它只是从头到尾，依次将每个英文单词用对应的中文含义来替换。对于每个英文单词，软件会先在内存中查找这个单词的中文含义，如果内存中有，软件就会用它进行翻译；如果内存中没有，软件就会在外存中的词典内查找，查出单词的中文含义然后翻译，并将这个单词和译义放入内存，以备后续的查找和翻译。

假设内存中有
M 个单元，每单元能存放一个单词和译义。每当软件将一个新单词存入内存前，如果当前内存中已存入的单词数不超过 M−1，软件会将新单词存入一个未使用的内存单元；若内存中已存入
M 个单词，软件会清空最早进入内存的那个单词，腾出单元来，存放新单词。

假设一篇英语文章的长度为
N 个单词。给定这篇待译文章，翻译软件需要去外存查找多少次词典？假设在翻译开始前，内存中没有任何单词。

输入格式

共 2 行。每行中两个数之间用一个空格隔开。
第一行为两个正整数 M,N，代表内存容量和文章的长度。
第二行为 N 个非负整数，按照文章的顺序，每个数（大小不超过 1000）代表一个英文单词。文章中两个单词是同一个单词，当且仅当它们对应的非负整数相同。

输出格式

一个整数，为软件需要查词典的次数。

输入数据 1

1
2
3

3 7
1 2 1 5 4 4 1

输出数据 1

提示

样例解释
整个查字典过程如下：每行表示一个单词的翻译，冒号前为本次翻译后的内存状况：

1.1：查找单词 1 并调入内存。
2.1 2：查找单词 2 并调入内存。
3.1 2：在内存中找到单词 1。
4.1 2 5：查找单词 5 并调入内存。
5.2 5 4：查找单词 4 并调入内存替代单词 1。
6.2 5 4：在内存中找到单词 4。
7.5 4 1：查找单词 1 并调入内存替代单词 2。
共计查了 5 次词典。

数据范围

对于
10% 的数据有 M=1，N≤5；
对于100% 的数据有1≤M≤100，1≤N≤1000。

解题思路（juju527的题解）

本人第一篇题解，运用c++语言（好像也只会c++）

先来下题目

假设内存中有 M 个单元，每单元能存放一个单词和译义。每当软件将一个新单词存入内存前，如果当前内存中已存入的单词数不超过 M−1 ，软件会将新单词存入一个未使用的内存单元；若内存中已存入 M 个单词，软件会清空最早进入内存的那个单词，腾出单元来，存放新单词。

假设一篇英语文章的长度为 N 个单词。给定这篇待译文章，翻译软件需要去外存查找多少次词典？假设在翻译开始前，内存中没有任何单词。

本题并不难，是2010年提高组里的水题，水水还是可以过的

我做这题的思路很简单，就是做出两个数组，一个放文章，一个放内存单元

接下来就是循环输入，及判断，并运用了一个自定义的寻找单词的函数

还有，测试点中有含0的样例，谨防入坑

样例代码（juju527的题解）

#include <bits/stdc++.h>
using namespace std;
int a[10000],b[1000],m,n,s=0,j=0;
int xz(int ddd){
	for(int i=1;i<=m;i++){
		if(b[i]==ddd)
		return 0;
	}
	return 1;
}
int main()
{
	cin>>m>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		if(a[i]==0)
		a[i]=-1;
		if(xz(a[i])==1){
			s++;
			if(j==m)
			j=0;
			j++;
			b[j]=a[i];
		}
	}
	cout<<s;
	return 0;
}

课后练习

Tea Queue

题面翻译

题面：

有n个学生排队喝茶。

第i 个学生在$l_i$的时刻来排队。如果在同一时刻有多名学生来排队，那么id 较大的学生就会在id 较小的学生之后。

队列中的学生的行为如下：如果学生面前没有人排队，那么他就用茶一秒钟，然后出队。否则会等待。如果第i 个学生在$r_i$的开始，仍然喝不到茶（队列前面有人），那么他就离开队伍了。

输入：

第一行：t，数据组数

每组数据的开头输入n，学生数

接下来n行每行为$l_i $, $r_i$

输出：

对于每组数据输出一行n个数，每个数表示这个学生喝到茶的时间，如果不能喝到就输出0

Translated by @@Lyrance

题目描述

Recently $ n $ students from city S moved to city P to attend a programming camp.

They moved there by train. In the evening, all students in the train decided that they want to drink some tea. Of course, no two people can use the same teapot simultaneously, so the students had to form a queue to get their tea.

$ i $ -th student comes to the end of the queue at the beginning of $ l{i} $ -th second. If there are multiple students coming to the queue in the same moment, then the student with greater index comes after the student with lesser index. Students in the queue behave as follows: if there is nobody in the queue before the student, then he uses the teapot for exactly one second and leaves the queue with his tea; otherwise the student waits for the people before him to get their tea. If at the beginning of $ r{i} $ -th second student $ i $ still cannot get his tea (there is someone before him in the queue), then he leaves the queue without getting any tea.

For each student determine the second he will use the teapot and get his tea (if he actually gets it).

输入格式

The first line contains one integer $ t $ — the number of test cases to solve ( $ 1<=t<=1000 $ ).

Then $ t $ test cases follow. The first line of each test case contains one integer $ n $ ( $ 1<=n<=1000 $ ) — the number of students.

Then $ n $ lines follow. Each line contains two integer $ l{i} $ , $ r{i} $ ( $ 1<=l{i}<=r{i}<=5000 $ ) — the second $ i $ -th student comes to the end of the queue, and the second he leaves the queue if he still cannot get his tea.

It is guaranteed that for every 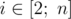condition $ l{i-1}<=l{i} $ holds.

The sum of $ n $ over all test cases doesn’t exceed $ 1000 $ .

Note that in hacks you have to set $ t=1 $ .

输出格式

For each test case print $ n $ integers. $ i $ -th of them must be equal to the second when $ i $ -th student gets his tea, or $ 0 $ if he leaves without tea.

样例 #1

样例输入 #1

样例输出 #1

1
2

1 2 
1 0 2

提示

The example contains $ 2 $ tests:

During $ 1 $ -st second, students $ 1 $ and $ 2 $ come to the queue, and student $ 1 $ gets his tea. Student $ 2 $ gets his tea during $ 2 $ -nd second.
During $ 1 $ -st second, students $ 1 $ and $ 2 $ come to the queue, student $ 1 $ gets his tea, and student $ 2 $ leaves without tea. During $ 2 $ -nd second, student $ 3 $ comes and gets his tea.

更多练习请见:这里